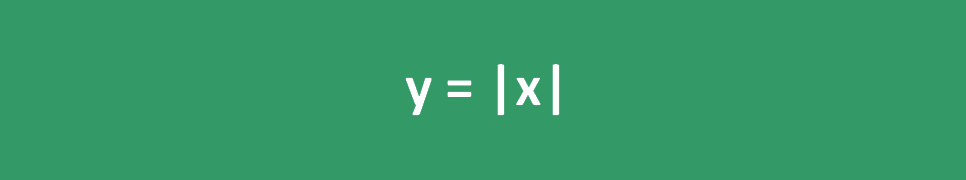Калькулятор абсолютного значения

The Калькулятор абсолютного значения быстро и легко вычисляет абсолютное значение введенного вами числа. При вводе любого числа, положительного или отрицательного, калькулятор покажет вам его абсолютное значение, расстояние от нуля. Этот онлайн-инструмент является идеальным решением для упрощения ваших математических операций и абсолютная ценность расчеты быстро. Используйте наш абсолютный искатель значений для ваших ежедневных расчетов.

Как рассчитывается абсолютное значение с помощью калькулятора абсолютных значений?

Используя Калькулятор абсолютного значения упрощает процесс нахождения абсолютного значения любого числа. Абсолютное значение — это значение, которое показывает, насколько число далеко от нуля, и всегда выражается как положительное. В математике абсолютное значение обычно представляется двумя вертикальными линиями: |x|.

Определение абсолютного значения:

1. Если число положительное (x > 0), его абсолютное значение равно ему самому. |x| = x
2. Если число равно нулю (x = 0), его абсолютное значение равно нулю. |0| = 0
3. Если число отрицательное (x < 0), его абсолютное значение является положительной формой числа. |x| = -x

Примеры:

• |5| = 5
• |-5| = 5
• |0| = 0

Применения абсолютного значения:

Абсолютное значение часто используется в математике и различных науках для вычисления расстояний, различий и ошибок. Например, абсолютное значение используется для нахождения величины разницы между двумя числами. Оно также часто встречается в таких областях, как финансы и инженерия.

Функция абсолютного значения также может быть представлена графически, как показано ниже: y = |x|

На этом графике точки с отрицательными значениями на оси x отображаются как положительные на оси y, и обе стороны графика симметричны относительно оси y.

Что такое абсолютное значение?

В математике, абсолютная ценность это расстояние числа от нуля и всегда принимает положительное значение. Абсолютное значение обычно представляется путем размещения вертикальных линий по обе стороны от числа: |x|. Абсолютное значение обрабатывает отрицательные и положительные числа одинаково, потому что имеет значение только величина, а не знак. Используйте нашу калькулятор абсолютного значения легко найти абсолютное значение любого числа.

Свойства абсолютного значения:

• Положительность: Абсолютное значение всегда больше или равно нулю.
• Симметрия: Абсолютные значения числа и его противоположного значения одинаковы. Например, |3| = 3 и |-3| = 3.
• Неравенство треугольника: |a + b| ≤ |a| + |b|, это свойство часто используется в алгебраических операциях.

Применения абсолютного значения:

Абсолютное значение используется в различных математических и научных приложениях. В частности, оно играет важную роль в расчетах расстояний, определении величины различий и анализе ошибок. Например, расстояние между двумя точками вычисляется как сумма абсолютных значений различий их координат.

Функция абсолютного значения представлена на графике как y = |x|, который симметричен относительно оси y.

Методы вычисления абсолютного значения

Абсолютное значение указывает расстояние числа от нуля и часто используется в математических вычислениях. Методы, используемые для вычисления абсолютного значения, основаны на основных математических правилах. Наш калькулятор абсолютного значения автоматизирует эти методы. Вы можете найти больше математических калькуляторов здесь.

1. Основной метод:

Для вычисления абсолютного значения применяются следующие правила:

• Если число положительное, то его абсолютное значение равно ему самому. |x| = x (если x ≥ 0)
• Если число отрицательное, его абсолютное значение — это его положительная форма. |x| = -x (если x < 0)

Примеры:

• Абсолютное значение положительного числа: |8| = 8
• Абсолютное значение отрицательного числа: |-8| = 8
• Абсолютное значение нуля: |0| = 0

Вычисление абсолютного значения с помощью алгебраических методов:

Абсолютное значение также может быть вычислено в некоторых математических операциях и уравнениях. Вот некоторые распространенные алгебраические методы:

Уравнения с абсолютным значением:

|х + 3| = 7

Это уравнение имеет два разных решения:

• х = 4, если х + 3 = 7
• x = -10, если x + 3 = -7

Неравенства с абсолютным значением:

|х – 2| < 5

Это неравенство распадается на следующие два неравенства:

-5 < х – 2 < 5

Это означает, что x < 7 и x > -3. Следовательно, -3 < x < 7

Неравенство треугольника:

Абсолютное значение суммы двух чисел меньше или равно сумме их абсолютных значений. |a + b| ≤ |a| + |b|

2. Графический метод:

Функция абсолютного значения на графике представлена V-образной кривой. График основной функции абсолютного значения определен как y = |x| и симметричен с вершиной в начале координат. Этот график имеет положительные значения с обеих сторон оси x.

3. Применяемые методы:

Абсолютное значение часто используется в реальных расчетах расстояний, анализе ошибок и в области науки о данных. Например, расстояние между двумя точками или погрешность измерения рассчитываются с использованием абсолютного значения.

Методы вычисления абсолютного значения играют важную роль в решении математических задач и развитии аналитических навыков.

Применения абсолютного значения в повседневной жизни

Абсолютное значение является важным понятием в математике, и мы сталкиваемся с ним в различных областях нашей повседневной жизни. Помня, что абсолютное значение — это положительное значение, которое указывает на расстояние числа от нуля, мы можем исследовать его различные применения.

1. Вычисление расстояний:

Абсолютное значение часто используется в расчетах расстояний. Например, при нахождении расстояния между двумя точками мы берем абсолютное значение разности их координат. Это обеспечивает, что расстояние всегда будет положительным.

Пример: При расчете расстояния между двумя городами используется абсолютное значение разницы их координат.

2. Анализ ошибок:

Абсолютное значение используется при анализе ошибок в измерениях. Абсолютное значение разницы между фактическим значением и измеренным значением показывает величину ошибки.

Пример: Абсолютное значение разницы между температурой, измеренной термометром, и реальной температурой дает ошибку измерения.

3. Финансы и экономика:

В финансовом анализе абсолютная величина используется для определения величины прибылей или убытков.