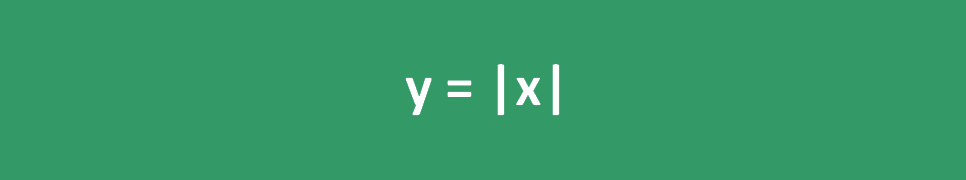Calculadora de valor absoluto

O Calculadora de valor absoluto calcula de forma rápida e fácil o valor absoluto do número que você insere. Ao inserir qualquer número, positivo ou negativo, a calculadora mostrará seu valor absoluto, a distância de zero. Esta ferramenta online é a solução ideal para simplificar suas operações matemáticas e fazer valor absoluto cálculos rapidamente. Use nosso localizador de valor absoluto para seus cálculos diários.

Como o valor absoluto é calculado com uma calculadora de valor absoluto?

Usando um Calculadora de valor absoluto simplifica o processo de encontrar o valor absoluto de qualquer número. Valor absoluto é um valor que indica o quão longe um número está de zero e é sempre expresso como positivo. Em matemática, o valor absoluto é geralmente representado por duas linhas verticais: |x|.

Definição de valor absoluto:

1. Se um número é positivo (x > 0), seu valor absoluto é ele mesmo. |x| = x
2. Se o número for zero (x = 0), seu valor absoluto é zero. |0| = 0
3. Se o número for negativo (x < 0), seu valor absoluto é a forma positiva do número. |x| = -x

Exemplos:

• |5| = 5
• |-5| = 5
• |0| = 0

Aplicações do valor absoluto:

O valor absoluto é frequentemente utilizado em matemática e em várias ciências para calcular distâncias, diferenças e taxas de erro. Por exemplo, o valor absoluto é utilizado para encontrar a magnitude da diferença entre dois números. Ele também é frequentemente encontrado em áreas como finanças e engenharia.

A função valor absoluto também pode ser representada por um gráfico como o abaixo: y = |x|

Neste gráfico, os pontos com valores negativos no eixo x são refletidos como positivos no eixo y, e ambos os lados do gráfico são simétricos em relação ao eixo y.

O que é valor absoluto?

Em matemática, valor absoluto é a distância de um número de zero e sempre assume um valor positivo. O valor absoluto é geralmente representado colocando linhas verticais em ambos os lados do número: |x|. O valor absoluto trata números negativos e positivos da mesma forma, porque é apenas a magnitude que importa, não o sinal. Use nosso calculadora de valor absoluto para encontrar facilmente o valor absoluto de qualquer número.

Propriedades do valor absoluto:

• Positividade: O valor absoluto é sempre maior ou igual a zero.
• Simetria: Os valores absolutos de um número e de seu oposto são os mesmos. Por exemplo, |3| = 3 e |-3| = 3.
• Desigualdade triangular: |a + b| ≤ |a| + |b|, essa propriedade é frequentemente usada em operações algébricas.

Usos do valor absoluto:

O valor absoluto é utilizado em várias aplicações matemáticas e científicas. Em particular, ele desempenha um papel importante nos cálculos de distância, na determinação da magnitude das diferenças e na análise de erros. Por exemplo, a distância entre dois pontos é calculada como a soma dos valores absolutos das diferenças de suas coordenadas.

A função valor absoluto é representada em um gráfico como y = |x|, que é simétrica em relação ao eixo y.

Métodos de cálculo do valor absoluto

Valor absoluto indica a distância de um número de zero e é frequentemente usado em cálculos matemáticos. Os métodos usados para calcular o valor absoluto são baseados em regras matemáticas básicas. Nosso calculadora de valor absoluto automatiza esses métodos. Você pode encontrar mais calculadoras matemáticas aqui.

1. Método básico:

As seguintes regras se aplicam para calcular o valor absoluto:

• Se um número é positivo, seu valor absoluto é ele mesmo. |x| = x (se x ≥ 0)
• Se um número for negativo, seu valor absoluto será sua forma positiva. |x| = -x (se x < 0)

Exemplos:

• O valor absoluto de um número positivo: |8| = 8
• O valor absoluto de um número negativo: |-8| = 8
• O valor absoluto de zero: |0| = 0

Cálculo do valor absoluto por métodos algébricos:

O valor absoluto também pode ser calculado em algumas operações e equações matemáticas. Aqui estão alguns métodos algébricos comuns:

Equações de valor absoluto:

|x + 3| = 7

Esta equação oferece duas soluções diferentes:

• x = 4 se x + 3 = 7
• x = -10 se x + 3 = -7

Desigualdades de valor absoluto:

|x – 2| < 5

Esta desigualdade se divide nas seguintes duas desigualdades:

-5 < x – 2 < 5

Isto significa que x < 7 e x > -3. Consequentemente -3 < x < 7

Desigualdade triangular:

O valor absoluto da soma de dois números é menor ou igual à soma dos seus valores absolutos. |a + b| ≤ |a| + |b|

2. Método gráfico:

A função valor absoluto é representada no gráfico como uma curva em forma de V. O gráfico da função básica de valor absoluto é definido como y = |x| e é simétrico com um vértice na origem. Este gráfico tem valores positivos dos dois lados do eixo x.

3. Métodos aplicados:

O valor absoluto é frequentemente usado em cálculos de distância da vida real, análise de erros e ciência de dados. Por exemplo, a distância entre dois pontos ou a margem de erro em uma medição é calculada com o valor absoluto.

Os métodos para calcular o valor absoluto desempenham um papel importante na resolução de problemas matemáticos e no desenvolvimento de habilidades de pensamento analítico.

Usos do valor absoluto na vida cotidiana

Valor absoluto é um conceito importante na matemática e o encontramos em vários campos do nosso cotidiano. Lembrando que o valor absoluto é um valor positivo que indica a distância de um número do zero, podemos explorar seus diferentes usos.

1. Cálculos de distância:

O valor absoluto é frequentemente usado em cálculos de distância. Por exemplo, ao encontrar a distância entre dois pontos, tomamos o valor absoluto da diferença de suas coordenadas. Isso garante que a distância seja sempre positiva.

Exemplo: Ao calcular a distância entre duas cidades, utiliza-se o valor absoluto das diferenças de suas coordenadas.

2. Análise de erro:

O valor absoluto é usado ao analisar erros em medições. O valor absoluto da diferença entre o valor real e o valor medido indica a magnitude do erro.

Exemplo: O valor absoluto da diferença entre a temperatura medida por um termômetro e a temperatura real dá o erro de medição.

3. Finanças e Economia:

Na análise financeira, o valor absoluto é usado para determinar a magnitude dos ganhos ou perdas