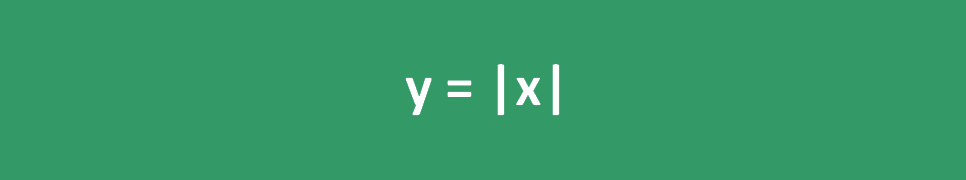Calculateur de valeur absolue

Le Calculateur de valeur absolue Calcule rapidement et facilement la valeur absolue du nombre saisi. En saisissant un nombre, positif ou négatif, la calculatrice affiche sa valeur absolue, c'est-à-dire sa distance à zéro. Cet outil en ligne est la solution idéale pour simplifier vos opérations mathématiques et vous aider à y parvenir. valeur absolue calculs rapidement. Utilisez notre chercheur de valeur absolue pour vos calculs quotidiens.

Comment la valeur absolue est-elle calculée avec un calculateur de valeur absolue ?

Utiliser un Calculateur de valeur absolue Simplifie la recherche de la valeur absolue d'un nombre. La valeur absolue indique la distance entre un nombre et zéro et est toujours exprimée positivement. En mathématiques, la valeur absolue est généralement représentée par deux lignes verticales : |x|.

Définition de la valeur absolue :

1. Si un nombre est positif (x > 0), sa valeur absolue est elle-même. |x| = x
2. Si le nombre est zéro (x = 0), sa valeur absolue est zéro. |0| = 0
3. Si le nombre est négatif (x < 0), sa valeur absolue est la forme positive du nombre. |x| = -x

Exemples:

• |5| = 5
• |-5| = 5
• |0| = 0

Applications de la valeur absolue :

La valeur absolue est souvent utilisée en mathématiques et dans diverses sciences pour calculer les distances, les différences et les taux d'erreur. Par exemple, la valeur absolue est utilisée pour trouver l'amplitude de la différence entre deux nombres. On la trouve également fréquemment dans des domaines tels que la finance et l'ingénierie.

La fonction de valeur absolue peut également être représentée par un graphique comme celui ci-dessous : y = |x|

Dans ce graphique, les points ayant des valeurs négatives sur l'axe des x sont reflétés sous forme positive sur l'axe des y et les deux côtés du graphique sont symétriques par rapport à l'axe des y.

Qu'est-ce que la valeur absolue ?

En mathématiques, valeur absolue est la distance d'un nombre à zéro et prend toujours une valeur positive. La valeur absolue est généralement représentée par des lignes verticales de chaque côté du nombre : |x|. La valeur absolue traite les nombres négatifs et positifs de la même manière, car seule la grandeur compte, et non le signe. Utilisez notre calculateur de valeur absolue pour trouver facilement la valeur absolue de n'importe quel nombre.

Propriétés de la valeur absolue :

• Positivité : La valeur absolue est toujours supérieure ou égale à zéro.
• Symétrie : Les valeurs absolues d'un nombre et de son opposé sont identiques. Par exemple, |3| = 3 et |-3| = 3.
• Inégalité triangulaire : |a + b| ≤ |a| + |b|, cette propriété est souvent utilisée dans les opérations algébriques.

Utilisations de la valeur absolue :

La valeur absolue est utilisée dans diverses applications mathématiques et scientifiques. En particulier, elle joue un rôle important dans les calculs de distance, la détermination de l'amplitude des différences et l'analyse des erreurs. Par exemple, la distance entre deux points est calculée comme la somme des valeurs absolues des différences de leurs coordonnées.

La fonction de valeur absolue est représentée sur un graphique sous la forme y = |x|, qui est symétrique par rapport à l'axe des y.

Méthodes de calcul de la valeur absolue

Valeur absolue Indique la distance d'un nombre à zéro et est fréquemment utilisé dans les calculs mathématiques. Les méthodes de calcul de la valeur absolue reposent sur des règles mathématiques élémentaires. Notre calculateur de valeur absolue automatise ces méthodes. Vous trouverez d'autres calculatrices mathématiques. ici.

1. Méthode de base :

Les règles suivantes s'appliquent pour calculer la valeur absolue :

• Si un nombre est positif, sa valeur absolue est elle-même. |x| = x (si x ≥ 0)
• Si un nombre est négatif, sa valeur absolue est sa forme positive. |x| = -x (si x < 0)

Exemples:

• La valeur absolue d'un nombre positif : |8| = 8
• La valeur absolue d'un nombre négatif : |-8| = 8
• La valeur absolue de zéro : |0| = 0

Calcul de la valeur absolue par méthodes algébriques :

La valeur absolue peut également être calculée dans certaines opérations et équations mathématiques. Voici quelques méthodes algébriques courantes :

Équations de valeur absolue :

|x + 3| = 7

Cette équation offre deux solutions différentes :

• x = 4 si x + 3 = 7
• x = -10 si x + 3 = -7

Inégalités de valeur absolue :

|x – 2| < 5

Cette inégalité se décompose en deux inégalités suivantes :

-5 < x – 2 < 5

Cela signifie que x < 7 et x > -3. Par conséquent, -3 < x < 7

Inégalité triangulaire :

La valeur absolue de la somme de deux nombres est inférieure ou égale à la somme de leurs valeurs absolues. |a + b| ≤ |a| + |b|

2. Méthode graphique :

La fonction de valeur absolue est représentée sur le graphique sous forme de courbe en forme de V. Le graphique de la fonction de valeur absolue de base est défini par y = |x| et est symétrique avec un sommet à l'origine. Ce graphique présente des valeurs positives des deux côtés de l'axe des x.

3. Méthodes appliquées :

La valeur absolue est souvent utilisée dans les calculs de distance dans la vie réelle, l'analyse des erreurs et la science des données. Par exemple, la distance entre deux points ou la marge d'erreur dans une mesure sont calculées avec la valeur absolue.

Les méthodes de calcul de la valeur absolue jouent un rôle important dans la résolution de problèmes mathématiques et le développement des compétences en pensée analytique.

Utilisations de la valeur absolue dans la vie quotidienne

Valeur absolue C'est un concept important en mathématiques, que nous rencontrons dans divers domaines de notre vie quotidienne. En gardant à l'esprit que la valeur absolue est une valeur positive indiquant la distance d'un nombre à zéro, nous pouvons explorer ses différentes utilisations.

1. Calculs de distance :

La valeur absolue est fréquemment utilisée dans les calculs de distance. Par exemple, lors du calcul de la distance entre deux points, nous prenons la valeur absolue de la différence de leurs coordonnées. Cela garantit que la distance est toujours positive.

Exemple : Lors du calcul de la distance entre deux villes, la valeur absolue de la différence de leurs coordonnées est utilisée.

2. Analyse des erreurs :

La valeur absolue est utilisée lors de l'analyse des erreurs dans les mesures. La valeur absolue de la différence entre la valeur réelle et la valeur mesurée indique l'ampleur de l'erreur.

Exemple : La valeur absolue de la différence entre la température mesurée par un thermomètre et la température réelle donne l'erreur de mesure.

3. Finance et économie :

Dans l’analyse financière, la valeur absolue est utilisée pour déterminer l’ampleur des gains ou des pertes