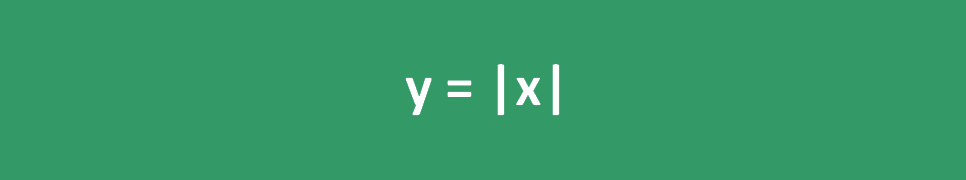حاسبة القيمة المطلقة
حاسبة القيمة المطلقة تحسب بسرعة وسهولة القيمة المطلقة للرقم الذي تدخله.
ال حاسبة القيمة المطلقة تحسب بسرعة وسهولة القيمة المطلقة للرقم الذي تُدخله. بإدخال أي رقم، سواءً كان موجبًا أم سالبًا، تُظهر لك الآلة الحاسبة قيمته المطلقة، أي المسافة من الصفر. تُعد هذه الأداة الإلكترونية الحل الأمثل لتبسيط عملياتك الحسابية وجعلها أكثر دقة. القيمة المطلقة حسابات سريعة. استخدم الباحث عن القيمة المطلقة لحساباتك اليومية.
جدول المحتويات:
كيف يتم حساب القيمة المطلقة باستخدام حاسبة القيمة المطلقة؟
باستخدام حاسبة القيمة المطلقة يُبسّط عملية إيجاد القيمة المطلقة لأي عدد. القيمة المطلقة هي قيمة تُشير إلى بُعد العدد عن الصفر، وتُعبّر عنها دائمًا برقم موجب. في الرياضيات، تُمثَّل القيمة المطلقة عادةً بخطين عموديين: |x|.
تعريف القيمة المطلقة:
- إذا كان الرقم موجبًا (x > 0)، فإن قيمته المطلقة هي نفسها. |x| = x
- إذا كان الرقم صفرًا (x = 0)، فإن قيمته المطلقة هي صفر. |0| = 0
- إذا كان الرقم سالبًا (x < 0)، فإن قيمته المطلقة هي الشكل الموجب للرقم. |x| = -x
أمثلة:
- |5| = 5
- |-5| = 5
- |0| = 0
تطبيقات القيمة المطلقة:
تستخدم القيمة المطلقة غالبًا في الرياضيات والعلوم المختلفة لحساب المسافات والفروق ومعدلات الخطأ. على سبيل المثال، يتم استخدام القيمة المطلقة لإيجاد مقدار الفرق بين رقمين. كما توجد أيضًا بشكل شائع في مجالات مثل المالية والهندسة.
يمكن أيضًا تمثيل دالة القيمة المطلقة بواسطة رسم بياني كما هو موضح أدناه: y = |x|
في هذا الرسم البياني، يتم عكس النقاط ذات القيم السلبية على المحور x لتصبح إيجابية على المحور y، وكلا جانبي الرسم البياني متماثلان بالنسبة للمحور y.
ما هي القيمة المطلقة؟
في الرياضيات، القيمة المطلقة هي المسافة بين الرقم والصفر، ودائمًا ما تكون موجبة. تُمثَّل القيمة المطلقة عادةً بوضع خطين عموديين على جانبي الرقم: |x|. تُعامل القيمة المطلقة الأعداد السالبة والموجبة بنفس الطريقة، لأن القيمة فقط هي المهمة، وليس الإشارة. استخدم حاسبة القيمة المطلقة للعثور بسهولة على القيمة المطلقة لأي رقم.
خصائص القيمة المطلقة:
- الإيجابية: القيمة المطلقة دائمًا أكبر من أو تساوي صفرًا.
- التماثل: القيم المطلقة لرقم وسالب الرقم هي نفسها. على سبيل المثال، |3| = 3 و |-3| = 3.
- متراجحة مثلثية: |a + b| ≤ |a| + |b|، يتم استخدام هذه الخاصية غالبًا في العمليات الجبرية.
استخدامات القيمة المطلقة:
تُستخدم القيمة المطلقة في العديد من التطبيقات الرياضية والعلمية. على وجه الخصوص، تلعب دورًا مهمًا في حساب المسافات، وتحديد حجم الفروق، وتحليل الأخطاء. على سبيل المثال، يتم حساب المسافة بين نقطتين باعتبارها مجموع القيم المطلقة لاختلافات إحداثياتهما.
تمثل دالة القيمة المطلقة على رسم بياني كـ y = |x|، وهي متماثلة بالنسبة للمحور y.
طرق حساب القيمة المطلقة
القيمة المطلقة يشير إلى بُعد الرقم عن الصفر، ويُستخدم بكثرة في الحسابات الرياضية. تعتمد طرق حساب القيمة المطلقة على قواعد رياضية أساسية. حاسبة القيمة المطلقة يُؤتمت هذه الطرق. يمكنك العثور على المزيد من الآلات الحاسبة الرياضية هنا.
1. الطريقة الأساسية:
تطبق القواعد التالية لحساب القيمة المطلقة:
- إذا كان الرقم موجبًا، فإن قيمته المطلقة هي نفسها. |x| = x (إذا كان x ≥ 0)
- إذا كان الرقم سالبًا، فإن قيمته المطلقة هي شكله الموجب. |x| = -x (إذا كان x < 0)
أمثلة:
- القيمة المطلقة لعدد موجب: |8| = 8
- القيمة المطلقة للعدد السالب: |-8| = 8
- القيمة المطلقة للصفر: |0| = 0
حساب القيمة المطلقة باستخدام الطرق الجبرية:
يمكن أيضًا حساب القيمة المطلقة في بعض العمليات والمعادلات الرياضية. إليك بعض الطرق الجبرية الشائعة:
معادلات القيمة المطلقة:
|س + 3| = 7
تقدم هذه المعادلة حلين مختلفين:
- x = 4 إذا x + 3 = 7
- x = -10 إذا كانت x + 3 = -7
عدم المساواة في القيمة المطلقة:
|x – 2| < 5
تتفكك هذه المعادلة إلى المعادلتين التاليتين:
-5 < x – 2 < 5
هذا يعني أن x < 7 و x > -3. وبالتالي، -3 < x < 7
متراجحة مثلثية:
القيمة المطلقة لمجموع عددين أقل من أو تساوي مجموع قيمتيهما المطلقتين. |a + b| ≤ |a| + |b|
2. الطريقة البيانية:
تمثل دالة القيمة المطلقة على الرسم البياني على شكل منحنى على هيئة حرف V. يتم تعريف رسم دالة القيمة المطلقة الأساسية على أنه y = |x| وهو متماثل مع قمة عند الأصل. يحتوي هذا الرسم على قيم موجبة على جانبي المحور السيني.
3. الطرق التطبيقية:
تستخدم القيمة المطلقة غالبًا في حسابات المسافات في الحياة الواقعية، وتحليل الأخطاء، وعلوم البيانات. على سبيل المثال، يتم حساب المسافة بين نقطتين أو هامش الخطأ في القياس باستخدام القيمة المطلقة.
تلعب طرق حساب القيمة المطلقة دورًا مهمًا في حل المشكلات الرياضية وتطوير مهارات التفكير التحليلي.
استخدامات القيمة المطلقة في الحياة اليومية
القيمة المطلقة يُعدّ مفهومًا مهمًا في الرياضيات، ونصادفه في مختلف مجالات حياتنا اليومية. وبما أن القيمة المطلقة قيمة موجبة تُشير إلى بُعد العدد عن الصفر، يُمكننا استكشاف استخداماتها المختلفة.
1. حساب المسافات:
تستخدم القيمة المطلقة بشكل متكرر في حسابات المسافة. على سبيل المثال، عند إيجاد المسافة بين نقطتين، نأخذ القيمة المطلقة لاختلاف إحداثياتهما. وهذا يضمن أن تكون المسافة دائمًا إيجابية.
مثال: عند حساب المسافة بين مدينتين، يتم استخدام القيمة المطلقة لاختلاف إحداثياتهما.
2. تحليل الأخطاء:
يتم استخدام القيمة المطلقة عند تحليل الأخطاء في القياسات. القيمة المطلقة لاختلاف القيمة الفعلية عن القيمة المقاسة تشير إلى حجم الخطأ.
مثال: القيمة المطلقة لاختلاف درجة الحرارة التي يقيسها مقياس الحرارة عن درجة الحرارة الفعلية تعطي خطأ القياس.
3. المالية والاقتصاد:
في التحليل المالي، يتم استخدام القيمة المطلقة لتحديد حجم المكاسب أو الخسائر